Contents

Markov property states that the future evolution of the stochastic process depends only on its current state, not depending on the passed transitions of the process. Otherwise, it is not Markovian.

However, in some cases, there is a way to transform a non-Markovian chain into a Markov chain, of course, with some cost.

k-denpendent Markov Chain

When the future evolution of a chain depends on more than its current state, but also \(k-1\) step(s) forward, this chain can be made into a Markov chain, at the cost of increasing the number of states.

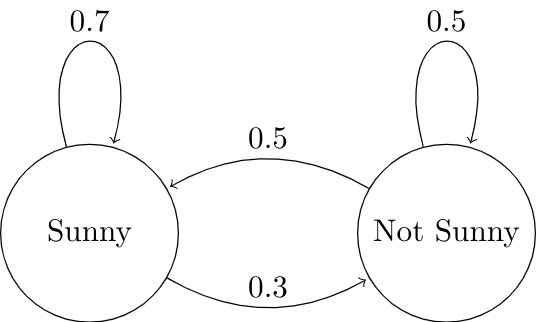
Example: city weather model

image

This is an image created with LaTeX using Overleaf.
Check for full LaTeX code snippet: 

        
\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{automata, positioning}
\begin{document}
    \begin{tikzpicture}
        \tikzset{state style/.style={state, minimum width=2cm}}
        \node[state style] (s) {Sunny};
        \node[state style, right=2 of s] (n) {Not Sunny};

        \draw[every loop]
            (s) edge[bend right, auto=left] node {0.3} (n)
            (n) edge[bend right, auto=right] node {0.5} (s)
            (s) edge[loop above] node {0.7} (s)
            (n) edge[loop above] node {0.5} (n);
    \end{tikzpicture}
\end{document}

This is a state diagram of a simple city weather model, categorizing the city weather into sunny and not-sunny states, supposing the weather of the next day depends only on the weather of the observing day. Obviously, the model is a Markov Chain.

Now consider a complicated model. The city weather is categorized into sunny and not-sunny states, and the weather of the next day depends on the weather of both the observing day and the day before the observing day. Clearly, it’s a non-Markovian situation.

However, it is possible the converting this chain into a Markov chain by increasing the number of states:

  • In the original model, observation at time step \(n+1\) depends on the state at both time step \(n\) and \(n-1\).
  • Now consider the combination of the observation at time step \(n+1\) and the state at time step \(n\) as the new defined observation at time step \(n+1\), that depends ONLY on a new defined state at time step \(n\) which is the combination of states at time step \(n\) and \(n-1\). Other settings of the original model remain the same.
  • In this modified model, the observation at time step \(n+1\), i.e. the consecutive weather status of the day \(n\) and \(n+1\), depends ONLY on the state at time step \(n\), i.e. the consecutive weather status of day \(n-1\) and \(n\).

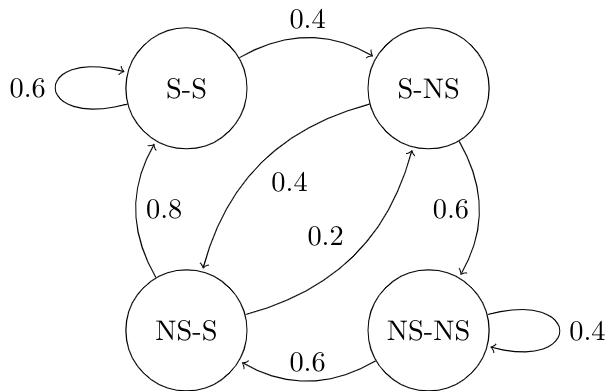
By applying this technique, the new model is a Markov chain with the number of states increased:

  • In the original model, the city weather is categorized into sunny and not-sunny states.
  • In the modified model, the city weather of two consecutive days is categorized into sunny/sunny, sunny/not-sunny, not-sunny/sunny and not-sunny/not-sunny states, the number of which is doubled.

Here is a sample state diagram of the modified model.

image

This is an image created with LaTeX using Overleaf.
Check for full LaTeX code snippet: 

        
\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{automata, positioning}
\begin{document}
    \begin{tikzpicture}
        \tikzset{state style/.style={state, minimum width=1.5cm}}
        \node[state style] at (0,0) (ss) {S-S};
        \node[state style] at (3,0) (sn) {S-NS};
        \node[state style] at (0,-3) (ns) {NS-S};
        \node[state style] at (3,-3) (nn) {NS-NS};

        \draw[every loop]
            (ss) edge[loop above] node {0.6} (ss)
            (ss) edge[bend left, auto=left] node {0.4} (sn)
            (sn) edge[bend right, auto=left] node {0.4} (ns)
            (sn) edge[bend left, auto=right] node {0.6} (nn)
            (ns) edge[bend left, auto=right] node {0.8} (ss)
            (ns) edge[bend right, auto=left] node {0.2} (sn)
            (nn) edge[loop below] node {0.4} (nn)
            (nn) edge[bend left, auto=right] node {0.6} (ns);
    \end{tikzpicture}
\end{document}

Generalized Technique

Reference

There are some books and articles I read while I was writing this post.1

  1. William J. Stewart, Probability, Markov Chains, Queues, and Simulation(The Mathematical Basis of Performance Modeling), 2009, Princeton University Press, Link. ↩