Contents

Markov Chain

  • Markov Process is a type of stochastic process with Markov Property.
  • Markov Chain is a type of Markov process with discrete state space.

Markov Property

Markov Property, i.e. Memoryless property, states that the future evolution of the process depends ONLY on its current state, not depending on the passed transitions of the process.

Discrete Time Markov Chain

  • Discrete Time Markov Chain(DTMC) is a type of Markov Chain with discrete parameter space.
graph LR; A(Stochastic Process)--Markov Property-->B(Markov Process); B--Discrete State Space-->C(Markov Chain); C--Discrete Parameter Space-->D(Discrete Time Markov Chain);

When we study the behavior of a DTMC, we observe its state at a discrete set of times. In practical applications, when transitions from state to state can only take place, or fail to take place at some time instants which are short enough to be omitted comparing to the time durations that the process stays in states, we could approximately observe the process at a discrete set of time.

  • When these time instants are mostly taken to be one unit apart, we could represent the discrete parameter space, or say index set \(T\) by the set of natural numbers \(\{0,1,2,\ldots \}\).
  • The successive observations define the set of \(r.v. X(t)\) which could also be represented with a set of \(\{X_0,X_1,X_2,\ldots ,X_n,\ldots \}\) at time instants \(0,1,2,\ldots ,n,\ldots\) respectively.

Mathematically, DTMC \(\{X_n, n=1,2,\ldots\}\) is a stochastic process that satisfies the Markov property, i.e. \(\forall n\) and \(\forall\) state \(x_n\),

\[\mathbf{Pr}(X_{n+1}=x_{n+1}\mid X_n=x_n, X_{n-1}=x_{n-1},\ldots ,X_0=x_0) \\ =\mathbf{Pr}(X_{n+1}=x_{n+1}\mid X_n=x_n)\]

Notation

States

For simplicity, we could use single letters, such as \(i, j, k, \ldots\), to represent the states instead of \(x_i, x_j, x_k, \ldots\).

(Single-step) Transition Probability

The single-step transition probability, or just the transition probability, of the Markov Chain is given by the conditional probability of making transition from state \(x_n=i\) to state \(x_{n+1}=j\) when the time parameter increases from \(n\) to \(n+1\), denoted as \(p_{ij}(n)=\mathbf{Pr}(X_{n+1}=j\mid X_n=i)\).

Transition Probability Matrix

The transition probability matrix, or chain matrix \(P(n)\) is the matrix formed with the transition probabilities \(p_{ij}(n)=\mathbf{Pr}(X_{n+1}=j\mid X_n=i)\) as the elements of row \(i\) and column \(j\) for all \(i\) and \(j\),

\[P(n)=\left( \begin{array}{cccccc} p_{00}(n) & p_{01}(n) & p_{02}(n) & \cdots & p_{0j}(n) & \cdots \\ p_{10}(n) & p_{11}(n) & p_{12}(n) & \cdots & p_{1j}(n) & \cdots \\ p_{20}(n) & p_{21}(n) & p_{22}(n) & \cdots & p_{2j}(n) & \cdots \\ \vdots & \vdots & \vdots & \ddots & \vdots & \cdots \\ p_{i0}(n) & p_{i1}(n) & p_{i2}(n) & \cdots & p_{ij}(n) & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{array} \right) \begin{array}{c} \dashrightarrow \sum{p_{0j}(n)} = 1 \\ \dashrightarrow \sum{p_{1j}(n)} = 1 \\ \dashrightarrow \sum{p_{2j}(n)} = 1 \\ \vdots \\ \dashrightarrow \sum{p_{ij}(n)} = 1 \\ \vdots \end{array}\]

elements of which satisfy \(\forall i,j\) \(0\leq p_{ij}(n)\leq 1\) and \(\sum_{all j}{p_{ij}(n)}=1\).

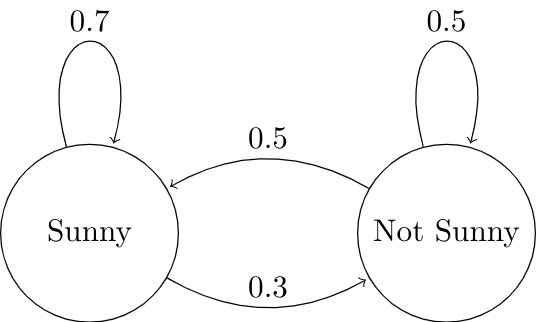
State Diagram

The behavior of the Markov chain is usually illustrated with state diagram, where

  • Circles are used to represent states,
  • Directed arrows with values are used to represent single-step transition from states to states,
  • Values of arrows are used to represent single-step transition probabilities respectively.
image

This is an image created with LaTeX using Overleaf.
Check for full LaTeX code snippet: 

        
\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{automata, positioning}
\begin{document}
    \begin{tikzpicture}
        \tikzset{state style/.style={state, minimum width=2cm}}
        \node[state style] (s) {Sunny};
        \node[state style, right=2 of s] (n) {Not Sunny};

        \draw[every loop]
            (s) edge[bend right, auto=left] node {0.3} (n)
            (n) edge[bend right, auto=right] node {0.5} (s)
            (s) edge[loop above] node {0.7} (s)
            (n) edge[loop above] node {0.5} (n);
    \end{tikzpicture}
\end{document}

This is a state diagram of a simple city weather model, categorizing the city weather into sunny and not-sunny states, supposing the weather of the next day depends only on the weather of the observing day. Obviously, the model is a Markov Chain.

graph LR; A((3))--1-->B((2)); B--2/3-->C((1)); C--1/3-->D((0)); D--1-->C; C--2/3-->B; B--1/3-->A;

This is a state diagram of Ehrenfest Model with \(N=3\), which is a simple, discrete model of the exchange of heat or gas molecules between two isolated bodies, by formulated as simple ball and urn model.

  • The balls correspond to the molecules, and there are \(N=3\) balls in the system in this case.
  • The urns correspond to the two isolated bodies, and the urns are labeled with 1 and 2.
  • At each time instant, a ball in the system is chosen at random and moved from the current urn to the other one.
  • Let \(r.v. X_n\) be the number of balls in the urn #1 after \(n^{th}\) selection, or \(n\) time steps.

Since the probability of different number of balls in urn #1 at time step \(n+1\) depends only on the number of balls in urn #1 at time step \(n\), the stochastic process \(\{X_n, n=1,2,\ldots\}\) is a Markov chain.

Further more in Markov Chain Example: Ehrenfest Model.

Non-Markovian Situation

Markov property states that the future evolution of the stochastic process depends only on its current state, not depending on the passed transitions of the process. Otherwise, it is not Markovian.

However, in some cases, there is a way to transform a non-Markovian chain into a Markov chain, of course, with some cost.

Further more in k-denpendent Markov Chains.

Time Dependency of DTMC

With any DTMC, we may study the time dependency of the system behavior through studying the relationship between the evolution of the system and the initial time or the elapsed time:

  • If DTMC is invariant under an arbitrary shift of time origin, it leads to the stationary property.
  • If the future evolution of DTMC is not depending on the elapsed time from initiation, it leads to the homogeneous property.
  • Note that the definition of DTMC states that the future evolution depending ONLY on its current state, not depending on the passed transitions of the process. However it doesn’t mean that the future evolution doesn’t depend on the elapsed time from initiation for certain.

Further more in Time Dependency of DTMC.

Reference

There are some books and articles I read while I was writing this post.1

  1. William J. Stewart, Probability, Markov Chains, Queues, and Simulation(The Mathematical Basis of Performance Modeling), 2009, Princeton University Press, Link. ↩